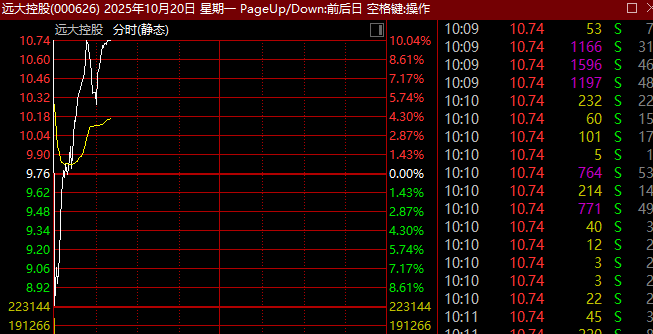
000626罕见“天地天板” 四连涨停后惊现逆转
罕见“天地天板”四连涨停后出现逆转,摘要为四连涨停后市场出现反转。
10月20日,A股三大指数开盘集体上涨。截至发稿,创业板指涨超3.5%,深证成指涨近2%。
盘面上,CPO、光芯片、保险、光通信、存储器概念等涨幅居前;黄金珠宝、贵金属等板块跌幅居前。
个股方面,远大控股(000626)盘中大幅波动,上演“天地天板”,现报10.25元,成交额超8亿元。该股此前走出4连板,今早以涨停开盘,随后快速跳水一度触及跌停。
港股方面,截至发稿,恒生指数涨超2%,恒生科技指数涨近3%。
科网股全线反弹,网易涨超5%,阿里巴巴涨近4%,腾讯控股、快手、美团、小米集团等涨超2%。港股半导体股多数走强,上海复旦涨超8%、中电华大科技、英诺赛科等涨近3%。
煤炭板块延续强势
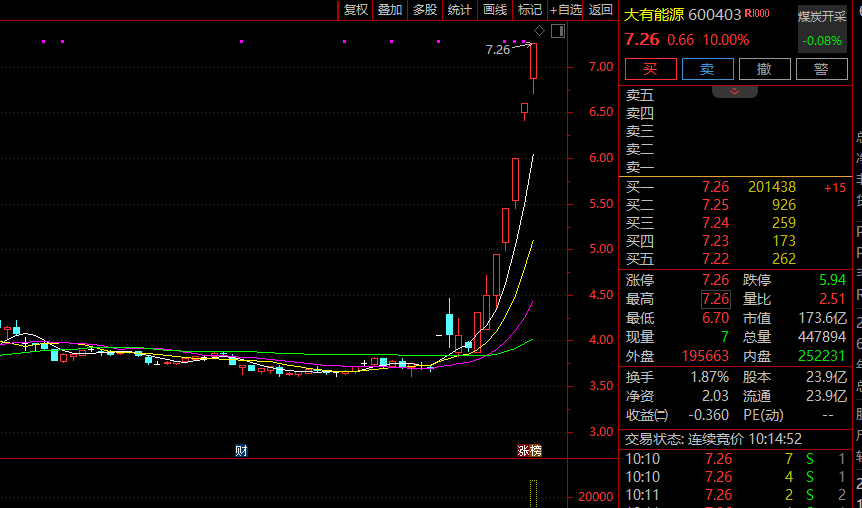
盘初,煤炭板块延续强势。大有能源走出11天7板,平煤股份、潞安环能、山西焦煤、晋控煤业、华阳股份等跟涨。
消息面上,国海煤炭开采行业周报显示,上周港口煤价环比提升明显,10月17日北方港口动力煤748元/吨(周环比上升39元/吨),山西、内蒙古、陕西坑口煤价分别环比上升50.00元/吨、45.00元/吨、46.00元/吨。
大有能源16日晚间公告,公司目前生产经营正常,市场环境、行业政策亦未发生重大调整。鉴于公司股票价格短期涨幅较大,股价剔除大盘和板块整体因素后的实际波动幅度较大,可能存在非理性炒作风险,请广大投资者注意二级市场交易风险,理性决策,审慎投资。
福建自贸区板块反复活跃,平潭发展2连板,海峡创新等跟涨。
消息面上,据世界航海装备大会组委会10月17日披露,在2025世界航海装备大会期间,福建省共对接签约项目172项、总投资超2000亿元。作为2025世界航海装备大会主要活动之一,10月16日于福州举办的福建省海洋经济产业合作创新发展大会上,集中签约海洋经济重大项目50个、总投资991.5亿元。
机器人概念再度走强,大洋电机涨停,三花智控、均普智能、东山精密、宁波华翔、安培龙跟涨。
消息面上,据报道,优必选中标“广西具身智能数据采集及测试中心设备采购及安装”项目,订单金额达1.26亿元。此外智元机器人精灵G2已获数亿元订单,并已开启首批商用交付。
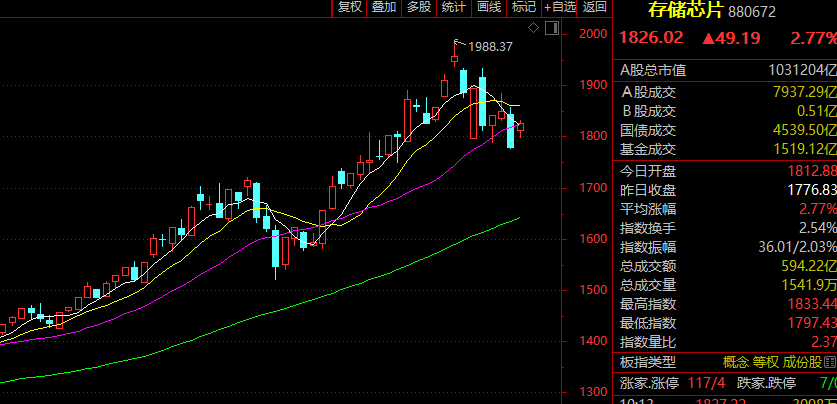
存储芯片板块拉升
存储芯片板块盘中拉升,三孚股份4连板,诚邦股份、万润科技涨停,聚辰股份、雅克科技、兆易创新、协创数据、恒烁股份跟涨。
机构研报指出,AI产品增长影响存储供需两端,四季度DRAM和NAND价格预计延续增长态势。本轮存储芯片的需求更多源自大型科技公司在AI时代的算力基建,持续性可能更强。
海南自贸区板块盘初冲高,海汽集团、凯撒旅业涨停,欣龙控股、海南机场、海南高速、海峡股份、海南发展跟涨。
消息面上,财政部、海关总署、税务总局联合印发公告,调整海南离岛旅客免税购物政策,并定于11月1日起实施。
另外,风电设备板块震荡走高,飞沃科技涨停,广大特材涨超6%,天能重工、盘古智能、海力风电跟涨。
工程机械板块走高,建设机械涨停,铁拓机械、恒立液压、唯万密封、中力股份、金道科技跟涨。